DNN深度神经网络的参数、结构对比
DNN深度神经网络的参数、结构对比
一、参数与结构
参数与结构主要是包含:
-
网络层数
-
不同隐含层个数
-
不同激活函数(隐含层的Sigmoid() 函数,Relu() 函数。注:输出层是统一的softmax()函数))
-
不同超参数(包含随机初始化权重值,学习率,训练(迭代)次数)
-
优化方法
二、网络层数
2.1 网络层数:
越来越深,输入层和输出层神经元个数不变,一个输入层一个输出层。保持学习率,隐含层神经元个数,激活函数、初始化权重值,训练次数不变。
| layer | 结果 |
|---|---|
| [784, 100, 10] | 收敛过程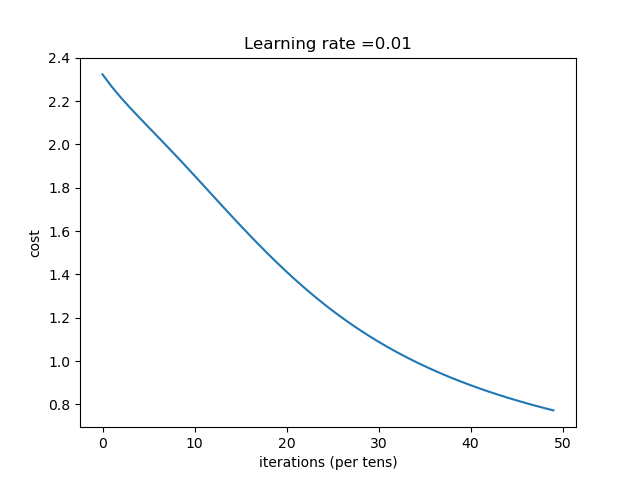 |
 |
学习结果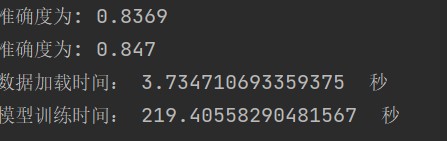 |
| 泛化能力 | |
| [784, 100, 75, 10] | 收敛过程: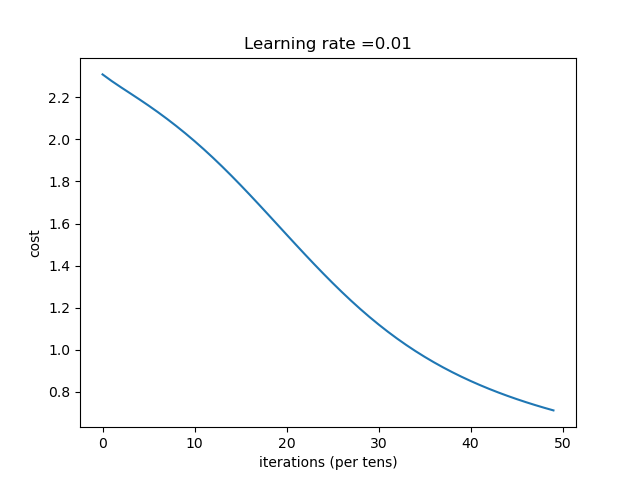 |
 |
学习结果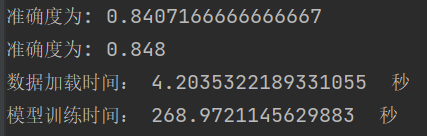 |
| 泛化能力 | |
| [784, 100, 75, 50,10] | 收敛过程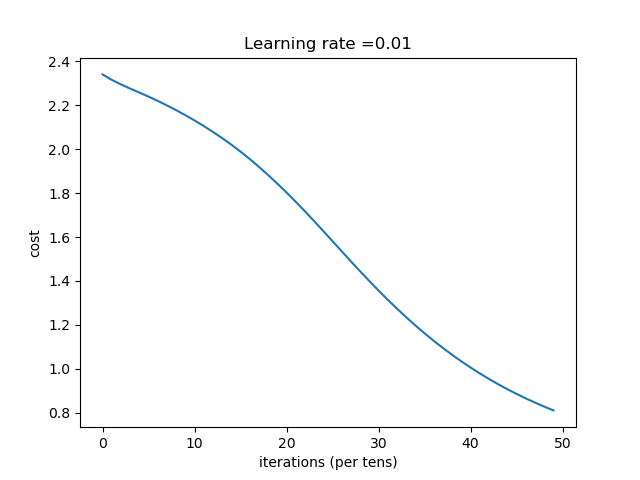 |
学习结果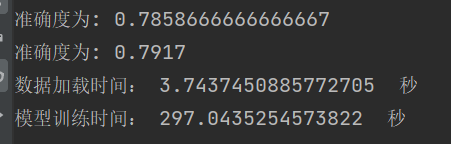 |
|
| 泛化能力 |
结论:网络越深,收敛的越慢,一定的深度增加测试集合的准确率和验证集的准确率。
2.2 不同隐含层神经元个数
增加隐含层神经元的个数,使用四层网络的结构,保持训练次数500,学习率0.01,使用relu激活函数。
| layer | 结果 |
|---|---|
| [784, 100, 75, 10] | 收敛过程 |
学习结果 |
|
| 泛化能力 | |
| [784, 200, 150, 10] | 收敛过程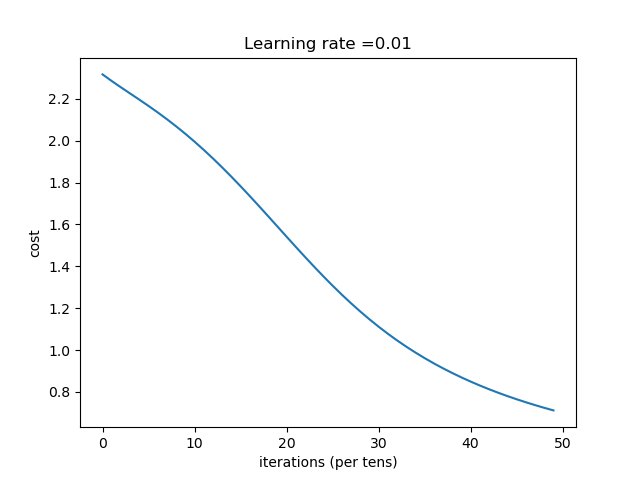 |
学习结果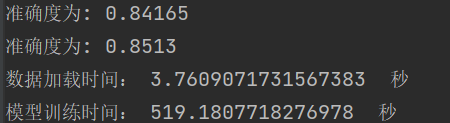 |
|
| 泛化能力 | |
| [784, 300,225,10] | 收敛过程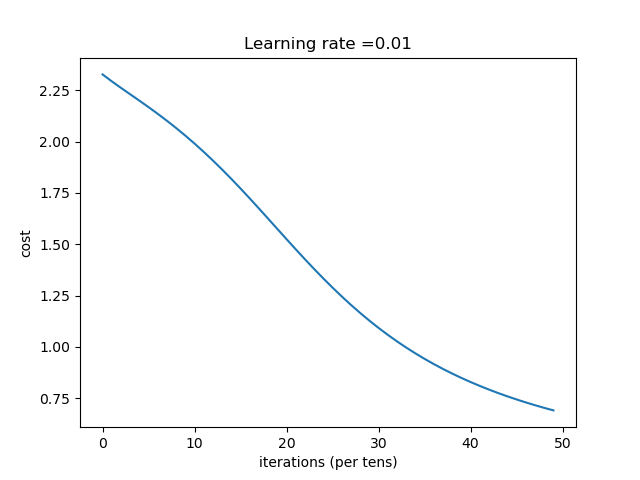 |
学习结果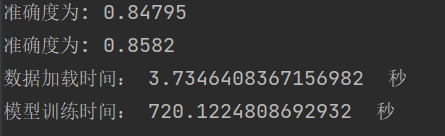 |
|
| 泛化能力 |
结论:随着隐含层的神经元个数的增加,
2.3 不同激活函数
(1)Sigmoid() 函数:
函数表达式:$$Sigmoid(x)=\frac{1}{1+e^{-x}}$$
代码实现:
1 | def sigmoid(Z): |
其导函数为:f(x)=1+e−x1=*ex*+1*ex*=1−(*e*x*+1)−1
代码实现:
1 | def sigmoid_backward(dA, cache): |
(2)Relu() 函数:
函数表达式:$$f\left( x \right) ,,=,,Max\left( 0,x \right) $$
代码实现:
1 | def relu(Z): |
其导函数为:$$
f\left( x \right) ’ =,,\begin{cases}
0 , x,,=,,0;\
1 , x,,\ne ,,0;\
\end{cases}
$$
代码实现:
1 | def relu_backward(dA, cache): |
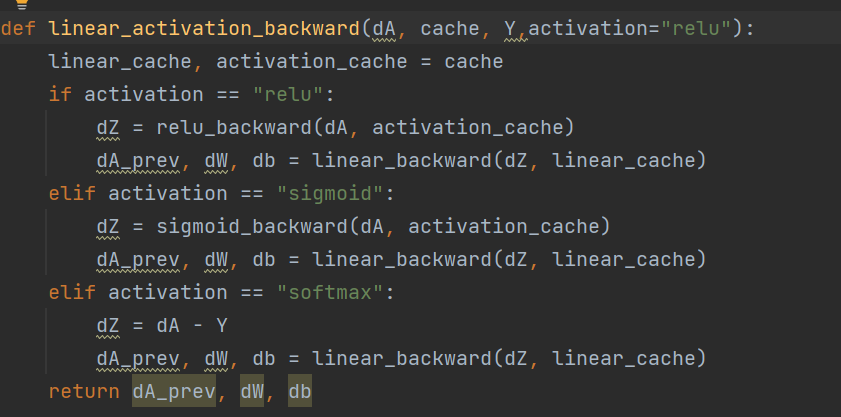
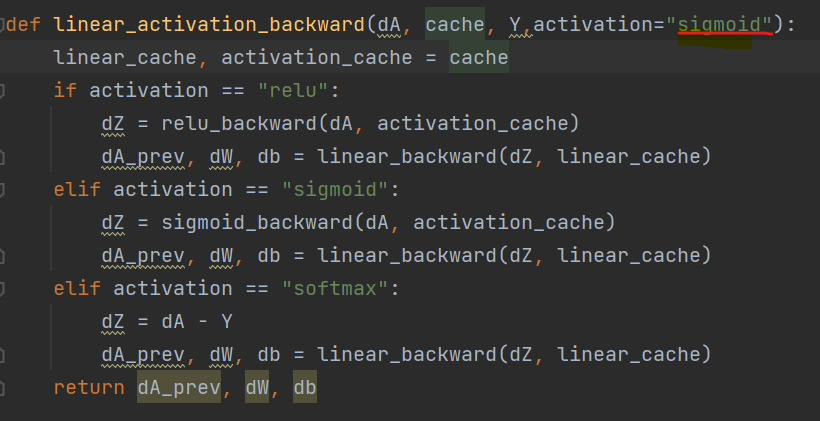
(3) 两个激活函数的对比
再相同的网络结构、参数下进行训练:[784, 100, 75, 10]
结果:
| relu() | sigmoid() | |
|---|---|---|
 |
 |
|
| 收敛过程: |  |
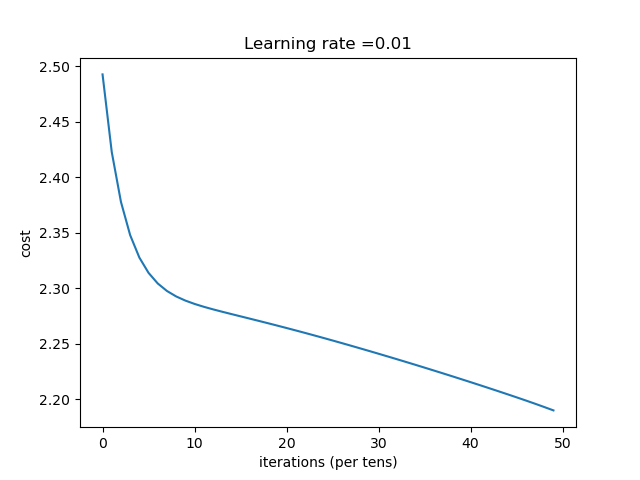 |
| 学习结果与泛化能力: |  |
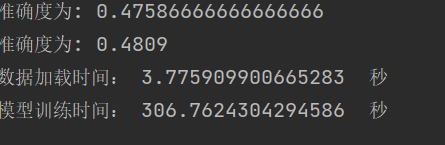 |
总结:一开始sigmoid()函数收敛快,但是到某一点的时候,收敛速度陡然下降,并几乎为一个常数。relu()函数则从开始到最后都保持一个很好的稳定性。且在MINIST数据集上,sigmod函数效果比relu函数的差。
2.4 不同超参数
(1)随机初始化权重值 (通过改变np.random.seed(3)随机种子值来设置初始化权重参数)
1 | def init_W(layers_dims): |
(2)学习率
改变代码中的learning_rate=0.0075(默认),改变学习率。
1 | def deepnet(X, Y,net_layers,learning_rate=0.0075, num_iterations=3000,step =1, print_cost=False, isPlot=True): |
使用网络结构为[784, 50,35,10],500的迭代次数。
| learning_rate | 结果 |
|---|---|
| 0.01 | 收敛过程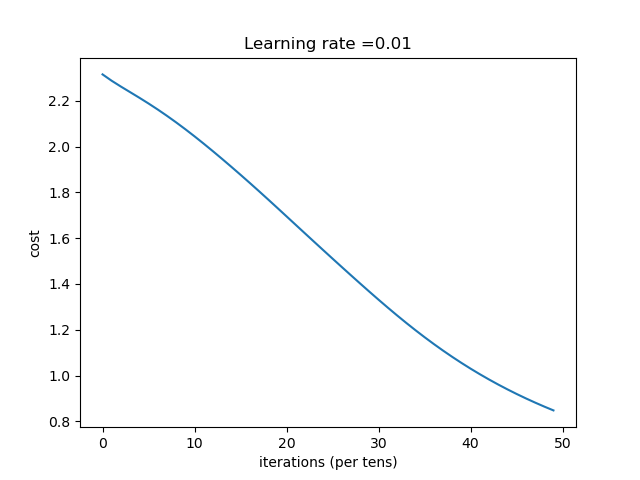 |
学习结果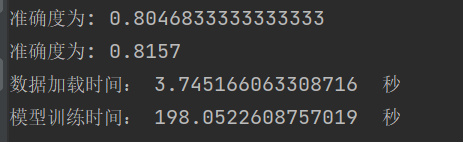 |
|
| 0.1 | 收敛过程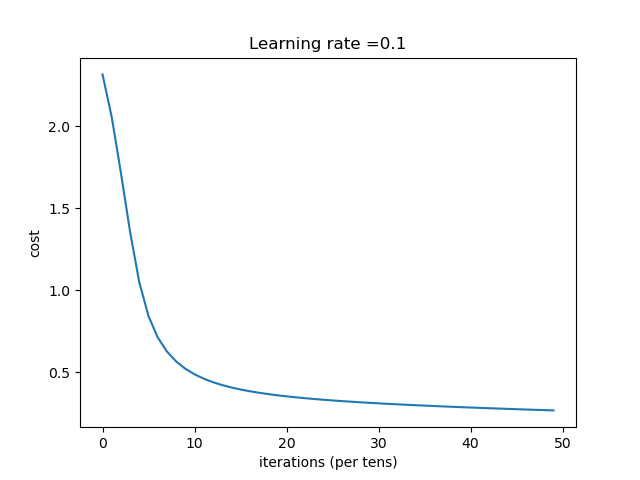 |
学习结果与泛化能力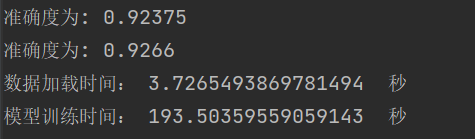 |
|
| 1 | 收敛过程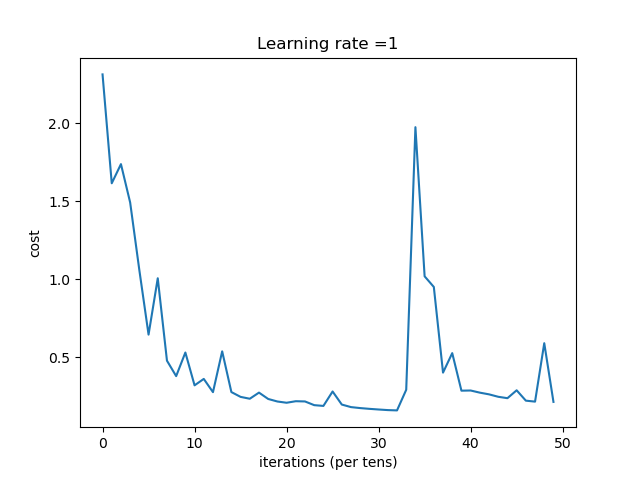 |
学习结果泛化能力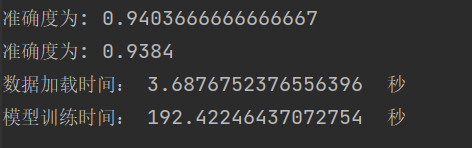 |
|
总结:学习率选择合适对网络非常重要,过小等于0.01时,收敛慢,过大等于1时导致在最优值左右摆动。
(3)训练(迭代)次数
改变代码中的num_iterations=3000,改变训练(迭代)次数。
1 | def deepnet(X, Y,net_layers,learning_rate=0.0075, num_iterations=3000,step =1, print_cost=False, isPlot=True): |
[784, 50,35,10]
| num_iterations | 结果 |
|---|---|
| 500 | 收敛过程 第 490 次迭代,成本值为: 0.21306134142390626 |
学习结果 |
|
| 泛化能力 | |
| 1000 | 收敛过程 第 950 次迭代,成本值为: 0.2089563048185612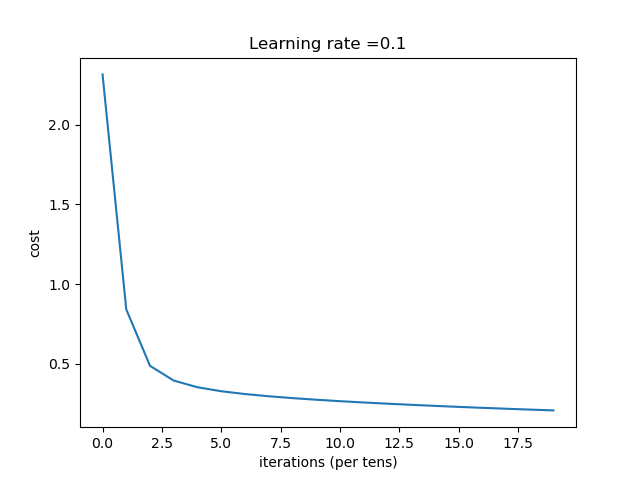 |
学习结果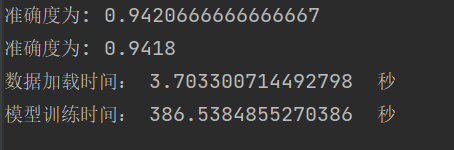 |
|
| 泛化能力 |
总结:在正常情况下,随着迭代次数的增多,网络效果越好。




